Презентация, доклад на тему история возникновения обыкновенных дробей

Сравнение дробей

1. Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
2. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
2. разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Слайд 18ИЗ ИСТОРИИ ОБОЗНАЧЕНИЯ ДРОБЕЙ. Современную систему записи дробей с числителем и знаменателем

создали в Индии. Только там писали знаменатель сверху, а числитель – снизу и не писали дробной черты. Записывать дроби в точности, как сейчас, стали арабы.В Древнем Китае пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. В XV веке, в Узбекистане математик и астроном Джемшид Гиясэддин ал –Каши записал дробь в одну строчку числами в десятичной системе и дал правила действия с ними. Он пользовался несколькими способами написания дроби: то он применял вертикальную черту, то чернила черного и красного цветов.

Слайд 12скрупулёзно — «скрупулус» Даже сейчас иногда говорят: «Он скрупулёзно изучил этот вопрос.»

Это значит, что вопрос изучен до конца, что не одной самой малой неясности не осталось. А происходит странное слово «скрупулёзно» от римского названия 1/288 асса — «скрупулус». В ходу были и такие названия: «семис»- половина асса, «секстанс»- шестая его доля, «семиунция»- половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.

Умножение и деление обыкновенных дробей

Прежде чем приступить к изучению вопроса об умножении и делении дробей, вспомним, что такое натуральные числа? А это те, которые начинаются с единицы — 1 и продолжаться могут до бесконечности. Но, к ним относятся только положительные числа, т.е, со знаком «+». Числа: -1; -2; -3; -4; -5 и т.д., натуральными не являются.

Для того, чтобы совершить действие умножения, нужно умножить числитель одной дроби на числитель другой и, соответственно, перемножить знаменатели. Что у нас получается? В результате вычисления (умножения) мы получаем дробь с числителем, который равен произведению числителей в дробях, и со знаменателем, равным произведению в дробях знаменателей.

Пример:

Умножается число 3 на число 7 (числители).  Умножаются знаменатель 5 на знаменатель 10. Записать данное действие можно двумя способами, это вы видите на картинке.

Пример умножения целого числа и дроби:

Целое число (2) записывается в виде дроби (2/1), в которой знаменателем будет единица (1).

Если нужно произвести деление дробей, поступают следующим образом: умножают первую дробь на перевернутую вторую.

Для простоты восприятия воспользуемся правилом сокращения: делим делитель и знаменатель на одинаковое число, например, дробь 21/63 выглядит не очень хорошо для восприятия, гораздо понятнее будет так — 1/3.

Делим смешанные числа:

Сначала их нужно представить неправильными дробями, затем, разделить друг на друга, вот, что получилось:

Пример:

Правильная и неправильная дробь

Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Обыкновенная дробь правильная неправильная

Еще дроби бывают правильными, например те, которые имеют такой вид — 2/8 и неправильными — 8/2 или 8/8. Возьмем неправильную дробь 41/5, читать ее следует так — восемь целых, одна пятая: 8 1/5. Это число называют смешанным, так как в нем отделяются целая часть и дробная. Другими словами мы наглядно видим сколько взяли целых тортов и сколько его частей. Чтобы ребенок осмысленно сокращал дроби, нужно показать ему это на практике и тогда он не будет ошибаться, сокращая дроби.

Для понимания: неправильная дробь трансформируется в целое число, сначала числитель делиться на знаменатель, в результате получается целое число (записывается, как целая часть) и остаток (записывается над чертой) в числитель. Знаменатель, при этом, не меняется.

К неправильным относят и те дроби, числитель и знаменатель которых, имеют одинаковое число, а при делении получается единица — 2/2, 3/3, 4/4 и т.д. Т.е., было взято столько кусков торта, на сколько его поделили.

Наглядно вы можете посмотреть на картинке:

Доклад №2

Дробь и посей день, остаётся одной из самых сложнейших глав математики. У них большая длинная и интересная история появления, которая исходит из глубин древности. Навыки разделять что-либо целое на части родилась на территории государств, древнего мира. Ежегодно действия происходящие с не целыми числами изменялись и совершенствовались. Раньше у каждых древних государств были свои умения создания и использования дробей как часть математики.

На первых парах дробями начали пользоваться египтяне, а также жители древнего Вавилона. Подход учёных в двух странах имели различия. Но необходимость использование дробей была и там и там. Первой из них стала ½ означающая половину. Позже возникли и другие четверть, треть и другие. Если обратится к информации учёных, история дробей началась ещё 5000 лет назад. Дроби чисел можно найти на папирусах в Египте и в Вавилоне.

Обыкновенные дроби не развивались в древней Греции. Греческие математики думали, что в должны существовать лишь целые. Поэтому выражения с дробями можно считать нигде практически не встречались. Ни на трактатах, ни на страницах книг.

В наше время мы используем десятичные дроби естественно и свободно, но в старое большее количество математиков усовершенствовали дроби. Например точку или запятую предложил использовать Непер в 1617 году.

На основании вышеперечисленных фактов можно сделать вывод, что дроби появились из за что нужно было делить целые числа и для решение бытовых и не только задач. Это удивительное изобретение человека, созданное в очень древнее время, для использование людей младших и старших возрастов, а также они используются и в других отраслях. Математика это наука помогающая совершать прогресс в различных науках.

Слайд 7Вавилонская нумерацияВ древнем Вавилоне примерно за 40 веков до нашего времени

создалась позиционная нумерация, то есть такой способ записи чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой. Наша теперешняя нумерация тоже поместная. В вавилонской поместной нумерации ту роль, которую у нас играет число 10, играет число 60, и потому эту нумерацию называют шестидесятиричной. Числа менее 60 обозначались с помощью двух знаков:  для единицы, и   для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например, — 3; — 3; — 30.

— это число 59.

1. Виды дробей

1.1. Обыкновенные дроби

Наглядное представление дроби

Обыкновенная (или простая) дробь — запись рационального числа в виде или . Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.

1.1.1. Обозначения обыкновенных дробей

Есть несколько видов записи обыкновенных дробей в печатном виде:

• ½
• 1/2 или 1 / ₂(наклонная черта называется «солидус»)
• выключная формула: (горизонтальная черта называется Винкулиум (англ.))
• строчная формула:

1.1.2. Правильные и неправильные дроби

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.

Например, дроби , и  — правильные дроби, в то время как , , и  — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.

1.1.3. Смешанные дроби

Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.

Например, . В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь.

1.1.4. Высота дроби

Высота обыкновенной дроби — модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.

Например, высота дроби равна 15 + 6 = 21. Высота же соответствующего рационального числа равна 5 + 2 = 7, так как дробь сокращается на 3.

1.1.5. Составные дроби

Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:

или или

1.2. Десятичные дроби

Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:

.

В данном случае часть, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Десятичная запись дроби всегда либо имеет конечное число знаков после запятой, либо является периодической дробью.

Чаще всего употребляется десятичная система счисления, хотя возможно применение любых других (в том числе и специфических, таких как фибоначчиева).

3. Действия над дробями

В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.

3.1. Приведение к общему знаменателю

Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: и . Порядок действий:

• Находим наименьшее общее кратное знаменателей: M = [b,d].
• Умножаем числитель и знаменатель первой дроби на M / b.
• Умножаем числитель и знаменатель второй дроби на M / d.

После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.

3.2. Сравнение

Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.

Пример. Сравниваем и . НОК(4, 5) = 20. Приводим дроби к знаменателю 20.

Следовательно,

3.3. Сложение и вычитание

Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:

+ = + =

НОК знаменателей (здесь 2 и 3) равно 6. Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Получилось . Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:

 — =  — =

НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем .

3.4. Умножение

Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:

В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:

3.5. Деление

Чтобы разделить одну обыкновенную дробь на другую, надо умножить первую на дробь, обратную второй:

Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель. Дробь, обратная , есть дробь , то есть число 3.

3.6. Преобразование между разными форматами записи

Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:

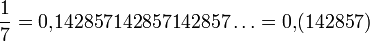— бесконечно повторяющийся период принято записывать в круглых скобках.

Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:

Слайд 6Шестидесятиричные дробиВ древнем Вавилоне предпочитали постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями,

унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями. Вместо слов «шестидесятые доли», «три тысячи шестисотые доли» говорили короче: «первые малые доли», «вторые малые доли». От этого и произошли наши слова «минута» (по латыни «меньшая») и «секунда» (по латыни «вторая»). Так что вавилонский способ обозначения дробей сохранил своё значение до сих пор.

Обыкновенные дроби 5 класс объяснение темы

Если ваш ребенок не понимает тему дробей, очень важно объяснить ему так же, как объясняют в классе и учитывать требования учителя. Детям самим не так просто самостоятельно понять все действия с дробями, задача родителей помочь и привести примеры, которые встречаются каждый день в повседневной жизни

Дайте ребенку шоколадку и попросите отломить от нее часть: целая — это единица, половина — одна вторая, а если плитку разломить на три части, это будет одна треть.

Чтобы лучше понять что такое дробь, нужно запомнить, что это значит — дробить. Когда мы режем торт, каждый кусок будет частью целого торта или очищаем мандарин, каждая долька — это часть целого мандарина. В обоих случаях, это доли целого. Не сложно привести и другие примеры, каждый день мы что-то режем, отделяем.

Арбуз разрезали на 6 частей, каждая часть (доля), это одна шестая от целого плода.

На этой картинке два мандарина. В одном оказалось 6 долек, в другом — 9.

На картинке ниже наглядно видно, как прописываются дроби:

Вот еще пример, желтый круг разрезали на 2 части, это будет одна вторая доли (1/2), зеленый — на 3 (1/3), синий — на 4 (1/4).

Итак, что нужно знать ребенку о дробях?

Чем на меньшее число поделено что-то целое, тем долей больше, а если на большее число, значит они меньше.

Слайд 4Во всех цивилизациях понятие дроби возникло из процесса дробления целого на

равные части. Русский термин «дробь», как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три – «треть», четыре – «четверть» и т. д.), для половины это не так – ее название во всех языках не имеет ничего общего со словом «два».Система записи дробей, правила действий с ними заметно различались как у разных народов, так и в разные времена у одного и того же народа. Важную роль играли также многочисленные заимствования идей при культурных контактах различных цивилизаций.

Слайд 11 Интересная система дробей была в Древнем Риме. Она основывалась

на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью — весом.

Дроби в Древнем Риме

1 тройская унция золота — мера веса драгоценных металлов

Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.

Слайд 10математический папирус Ринда Как использовались дроби в Древнем Египте, позволила нам

узнать расшифровка папирусного свитка, найденного в Луксоре в 1858 г. Генрихом Риндом. Сейчас этот свиток находится в Британском музее в Лондоне. Папирус Ринда был написан писцом по имени Ахмес примерно в 1650 г. до нашей эры. Это математическая рукопись, составленная учителем для своих учеников, готовившихся стать придворными писцами.

В папирусе есть задача: разделить семь хлебов между восемью людьми. Если резать каждый хлеб на 8 частей, придётся сделать 49 разрезов. А по–египетски эта задача решалась так. Дробь 7/8 записывали в виде долей: ½+1/4+1/8. Теперь ясно, что надо 4 хлеба разрезать пополам, 2 хлеба на 4 части и только один хлеб – на 8 частей (всего 17 разрезов).

Обыкновенные дроби: история возникновения, понятие, применение и свойства

В данном исследовательском проекте по математике на тему «Обыкновенные дроби в жизни людей» автор изучает историю возникновения дробей, даёт определение «обыкновенная дробь», а также наглядно показывает обыкновенные дроби.

Подробнее о проекте:

В авторском исследовательском проекте по математике «Обыкновенные дроби в жизни людей» ученик 5 класса стремится показать, что дроби нужны не только в математике, но и в повседневной жизни. Учащийся дает развернутое определение понятия «дроби в математике», а также приводит подробную характеристику обыкновенных дробей.

Введение

С первого знакомства с дробями было понятно, что они очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними.

В обычной жизни, и взрослым, и детям каждый день приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа, что является актуальностью данной темы.

Мне стало интересно узнать: как и когда появились дроби? В какой сфере жизни больше всего практически их применяют? Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни.

Объект исследования: обыкновенные дроби

Предмет исследования: использование дробей в нашей повседневной жизни.

Цель: показать, что дроби нужны не только в математике, но и в повседневной жизни.

1. Узнать, что такое дробь, какие виды дроби существуют
2. Изучить историю возникновения дробей.
3. Рассмотреть применение дробей в повседневной жизни.
4. Оценить достижения науки в данной области.

Обыкновенные дроби сложение вычитание

Правила сложения

Начнем с дробей, у которых одинаковые знаменатели, это самое простое вычисление — высчитывается сумма только числителей — тех чисел, которые находятся над черточкой.

Например:

Можно записать и так:

Немного сложней выполнить действие сложения, если знаменатели разные. В этом случае необходимо сначала:

Пример:

Далее:

Затем, каждую часть дроби, знаменатель и числитель, нужно умножить на свой множитель, который мы определили:

Далее производим сложение дробей:

Правила вычитания

Действие производится аналогичным образом, если у дроби знаменатели одинаковые, необходимо найти разность числителей.

Если у дроби знаменатели разные, Так же, как и при сложении, находим наименьшее кратное число.

Слайд 24Список использованных источников и литературы 1. Виленкин Н.Я., Жохов А.С.,

Чесноков А.С., Шварцбурд С.И. Математика: Учебник для 5 класса общеобразовательных учреждений. –
М.: Мнемозина, 2013г.
2. Перельман Я.И. Живая математика.
3. http://funnymath.ru 4. http://udivit-matem.narod.ru 5. http://mathworld.ru 6.Энциклопедия для детей. Том 11. Математика. Москва, «Аванта+»,1998.
7. http://ru.wikipedia.org/wiki.Материал из Википедии — свободной энциклопедии.8.Виленкин Н.Я. « Из истории дробей».9.wwwwww.www.referatworkwww.referatwork.www.referatwork.ru 10.http://storyof.ru/chisla/istoriya-poyavleniya-matematicheskoj-drobi/11.http://freecode.pspo.perm.ru/436/work/ss/ist_ch.html/12.http://revolution.allbest.ru/mathematics/ 13. http://www.researcher.ru/methodics/teor/   

Слайд 6НА ПРОТЯЖЕНИИ МНОГИХ ВЕКОВ НА ЯЗЫКАХ НАРОДОВ ЛОМАНЫМ ЧИСЛОМ ИМЕНОВАЛИ

ДРОБЬ. НЕОБХОДИМОСТЬ В ДРОБЯХ ВОЗНИКЛА НА РАННЕЙ СТУПЕНИ РАЗВИТИЯ ЧЕЛОВЕЧЕСТВА. ТАК, ПО-ВИДИМОМУ, ДЕЛЕЖ ДЕСЯТКА ПЛОДОВ МЕЖДУ БОЛЬШИМ ЧИСЛОМ УЧАСТНИКОВ ОХОТЫ ЗАСТАВЛЯЛ ЛЮДЕЙ ОБРАЩАТЬСЯ К ДРОБЯМ. ПЕРВОЙ ДРОБЬЮ БЫЛА ПОЛОВИНА. ДЛЯ ТОГО, ЧТОБЫ ИЗ ОДНОГО ПОЛУЧИТЬ ПОЛОВИНУ, НАДО РАЗДЕЛИТЬ ЕДИНИЦУ, ИЛИ «РАЗЛОМИТЬ» ЕЕ НА ДВА.
ОТ СЮДА И ПОШЛО НАЗВАНИЕ ЛОМАНЫЕ ЧИСЛА. ТЕПЕРЬ ИХ НАЗЫВАЮТ ДРОБЯМИ.
РАЗЛИЧАЮТ ТРИ ВИДА ДРОБЕЙ:
ЕДИНИЧНЫЕ (АЛИКВОТЫ) ИЛИ ДОЛИ (НАПРИМЕР, 1/2, 1/3, 1/4, И Т.Д.).
СИСТЕМАТИЧЕСКИЕ, Т.Е ДРОБИ, У КОТОРЫХ ЗНАМЕНАТЕЛЬ ВЫРАЖАЕТСЯ СТЕПЕНЬЮ ЧИСЛА (НАПРИМЕР, СТЕПЕНЬЮ ЧИСЛА 10 ИЛИ 60 И Т.Д.).
ОБЩЕГО ВИДА, У КОТОРЫХ ЧИСЛИТЕЛЕМ И ЗНАМЕНАТЕЛЕМ МОЖЕТ БЫТЬ ЛЮБОЕ ЧИСЛО.
СУЩЕСТВУЮТ ДРОБИ «ЛОЖНЫЕ» – НЕПРАВИЛЬНЫЕ И «РЕАЛЬНЫЕ» – ПРАВИЛЬНЫЕ.

Слайд 3Из истории возникновения обыкновенных дробей В жизни человеку

приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага. Появление дробей связано у многих народов с делением добычи на охоте. В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин.

Слайд 23Заключение Учение о дробях считалось самым трудным разделом математики

во все времена и у всех народов. Кто знал дроби, был в почете. Я сделала вывод, что история обыкновенных дробей — это извилистая дорога со многими препятствиями и трудностями. При работе я узнала много нового и интересного. В результате работы над проектом я узнала историю развития обыкновенных дробей, сумела рассмотреть задачи древности, связанные с дробями и задачи с практическим содержанием. Особый интерес при работе над проектом я испытала при решении старинных задач с использованием дробей.
Считаю, что материалы моей работы будут интересными для других учащихся. Они могут быть использованы как на уроке, так и для проведения внеклассных мероприятий по математике.