Осевая и центральная симметрия

Введение

«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе»

Л.Н. Толстой

Объект исследования – симметрия.

Предмет исследования – симметрия в жизни.

Цель работы: выяснить, как проявляется симметрия в жизни.

Для достижения поставленной цели необходимо выполнить следующие задачи:

1. Дать общее понятие о симметрии, о видах симметрии, симметрии в жизни.
2. Сделать фотографии всего, что мы можем и проанализировать, симметричны ли они, найти оси и центры симметрии.
3. Продемонстрировать, как будут выглядеть одежды, если их одежды будут не симметричные относительно левой и правой части.
4. Представить результаты наблюдения в презентации.

Гипотеза исследования: симметрия это — гармония и красота, равновесие, устойчивость.

Методы исследования:

1. Анализ статей о симметрии в жизни.
2. Наблюдение.
3. Компьютерное моделирование (обработка фотографий средствами графического редактора).
4. Обобщение и систематизация полученных данных.

Этапы работы:

1. Подготовительный. Изучение литературы, составление плана.
2. Основной. Сбор информации, фотосъёмка, обработка фотографий.
3. Заключительный. Систематизация полученной информации, составление презентации.

Актуальность темы. Тема проекта по математике «Симметрия в жизни» очень актуальна и интересна. В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живем, наполнен симметрией домов и улиц, гор и полей, творениями природы и человека.

С симметрией мы встречаемся буквально на каждом шагу: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.

Содержание

• Слайд 1

• Слайд 2

• Слайд 3

  • Понятие симметрии хорошо знакомо и играет важную роль в повседневной жизни. Многим творениям человеческих рук умышленно придается симметричная форма как из эстетических, так и практических соображений.
  • В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, одинаковость в расположении частей».

• Слайд 4

  • Зеркальная симметрия
  • Двусторонняя симметрия
  • Осевая симметрия
  • Параллельный перенос
  • Центральная симметрия

• Слайд 5

  • Отражательная симметрия или осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.
  • Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет.
  • Применительно к плоскости эти оба вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).

• Слайд 6

• Слайд 7

• Слайд 8

• Слайд 9

• Слайд 10

  • Двусторонняя симметрия — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Если на плоскость симметрии опустить перпендикуляр из точки а и и затем из точки О на плоскости симметрии продолжить его на длину аО, то он попадёт в точку а1, во всем подобную точке а. Ось симметрии у билатерально симметричных объектов отсутствует. У животных билатеральная симметрия проявляется в схожести или почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, различия в папиллярных линиях, ветвлении сосудов и расположении родинок на правой и левой руках человека). Часто существуют небольшие, но закономерные различия во внешнем строении (например, более развитая мускулатура правой руки у праворуких людей) и более существенные различия между правой и левой половиной тела в расположении внутренних органов. Например, сердце у млекопитающих обычно размещено несимметрично, со смещением влево.
  • У животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых- форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными.

• Слайд 11

• Слайд 12

  Зеркальная симметрия, это вид симметрии, часто наблюдаемый в природе и в созданных человеком вещах, — так называемая зеркальная симметрия. Человеческое тело обладает (приближенно) зеркальной симметрией относительно вертикальной оси. В зеркале правая и левая руки и другие части тела меняются местами, но видимое нами зеркальное отражение узнаваемо. Многие архитектурные сооружения, например арки или соборы, обладают зеркальной симметрией.

• Слайд 13

• Слайд 14

• Слайд 15

• Слайд 16

• Слайд 17

• Слайд 18

  Центральная симметрия

  Симметрия относительно точки или центральная симметрия — это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.

• Слайд 19

• Слайд 20

• Слайд 21

• Слайд 22

• Слайд 23

• Слайд 24

Посмотреть все слайды

Снежинки

Даже такие крошечные вещи как снежинки тоже образуются по законам порядка, так как большинство снежинок формируются в виде шестикратной радиальной симметрии со сложными, идентичными рисунками на каждой из её ветвей.

Понять, почему растения и животные выбирают симметрию, сложно само по себе, но неодушевлённые объекты – как же им это удаётся? По-видимому, всё сводится к химии, и в частности к тому, как молекулы воды выстраиваются по мере своего замерзания (кристаллизуются).

Молекулы воды приходят в твёрдое состояние путём образования слабых водородных связей друг с другом. Эти связи выравниваются в упорядоченном расположении, которое максимизирует силы притяжения и снижает силы отталкивания, что как раз и является причиной образования гексагональной формы снежинки. Однако всем нам известно, что двух одинаковых снежинок не бывает, так как же снежинка формируется в абсолютной симметрии сама с собой, но не похожа на другие снежинки? По мере того как каждая снежинка падает с неба она проходит через уникальные атмосферные условия, такие как температура и влажность, которые влияют на то, как кристаллы «растут» на ней. Все ветви снежинки проходят через одни и те же условия и следовательно кристаллизуются одинаковым образом — каждая ветвь является точной копией другой. Ни одна другая снежинка не проходит через те же условия по мере своего спуска, поэтому они все выглядят немного по-разному.

О жизни и творчестве

• Арзамасцева И. Н. Антоний Погорельский // Детская литература : учебник для вузов и средних педагогических учебных заведений / И. Н. Арзамасцева, С. А. Николаева. — Москва : Academia : Высшая школа, 2000. — С. 113–117.
• Коровин, В. Антоний Погорельский (Алексей Алексеевич Перовский) : (1787–1836) / В. Коровин // Антология мировой детской литературы. — Москва : АВАНТА+. — 2002. — Т. 5. — С. 380–382.
• Русские писатели : биобиблиографический словарь. : в двух частях : Часть 2 : М – Я / под редакцией П. А. Николаева. — Москва : Просвещение. — 1990. — 446 с. : 4 л. портр. — (Библиотека учителя русского языка и литературы).
• Светлова, Г. Друг Пушкина Анатолий Погорельский / Г. Светлова // Дошкольное воспитание. — 2003. — N 2. — С. 61–64. — Ил. — (В мире прекрасного).
• Турьян, М. Жизнь и творчество Антония Погорельского : вступительная статья / М. Турьян // Избранное / А. Погорельский. — Москва : Советская Россия, 1985. – С. 3–22.
• Турьян, М. А. Личность А. А. Перовского и литературное наследие Антония Погорельского / М. А. Турьян // Погорельский, А. Сочинения. Письма / Антоний Погорельский ; подгот. изд. М. А. Турьян ; отв. ред. Б. Ф. Егоров. — Санкт-Петербург : Наука, 2010.
• Шаров, А. И. Антоний Погорельский // Волшебники приходят к людям : книга о сказке и о сказочниках /Александр Шаров ; худож. Ника Гольц. — Санкт-Петербург ; Москва : Речь, 2020. — С. 82–104.
• Шевляков, А. И. Волшебное семечко: Пьеса по сказке А. Погорельского «Чёрная Курица, или Подземные жители» / А. И. Шевляков // Театр круглый год. — 2006. — Вып. № 4. — С. 21–25.
• Шелаева, А. А. Антоний Погорельский и его сочинения : послесловие / А. А. Шелаева // Избранное / А. Погорельский. — Москва: Правда, 1988. — С. 373–389.
• Горленко, Василий Петрович (1853–1907). Алексей Алексеевич Перовский Текст : электронный ресурс : биографический очерк / В. Горленко. — Киев : тип. Г. Т. Корчак-Новицкого, 1888. — 16 с. Оригинал хранится в РГБ. — Режим доступа: Открытый доступ (дата обращения 26.07.2019)
• Кирпичников А. И. Перовский, Алексей Алексеевич Текст : электронный ресурс : биографический очерк // Русский биографический словарь А. А. Половцова. — Режим доступа : Открытый доступ (дата обращения 26.07.2019)
• Малая С. Погорельский Антоний Текст : электронный ресурс / Светлана Малая // Библиогид. — Режим доступа: Открытый доступ (дата обращения 26.07.2019)
• Подосокорский Н. Н. «Черная курица, или Подземные жители» Антония Погорельского как повесть о масонской инициации Текст : электронный ресурс // Вопросы литературы. — 2012. — № 5. — С. 124-144. — (Над строками одного произведения)
• — RU RGDB\BIBL\240026. Татаринова Н. Н. Перовский Алексей Алексеевич (Антоний Погорельский) (1787–1836) Текст : Электронный ресурс / Н. Н. Татаринова // Материалы по истории русской детской литературы (1750-1855). Вып.1 / под редакцией А. К. Покровской и Н. В. Чехова; Институт методов внешкольной работы, Отдел детского чтения. — Москва : Издание ИМВР, 1927. — С. 151–156. — (Труды комиссии по истории русской детской литературы ; Т. 1). — Режим доступа: Открытый доступ
• Турьян, М. А. О «Черной курице» Антония Погорельского Текст : электронный ресурс / М. А. Турьян // И время и место : историко-филол. сборник к шестидесятилетию Александра Львовича Осповата / сост. Рональд Вроон ; издатель А. Р. Курилкин. — Москва : Новое издательство, 2008. — Режим доступа: Открытый доступ (дата обращения 26.07.2019)

Виды симметрии

Вид симметрии	Определение	Пример
Лучевая	Расположение частей тела, позволяющее разделить его на 2 равные, зеркально отражающие друг друга половины в нескольких плоскостях.
Билатеральная (осевая)	Расположение частей тела, позволяющее разделить его на две равные, зеркально отражающие друг друга половины лишь одной плоскостью. Эта плоскость носит название оси симметрии.
Центральная	Симметрия относительно точки. Предполагает, что по обе стороны от точки, на одинаковых расстояниях находится какой либо предмет.
Зеркальная	Зеркальная симметрия в архитектуре и природе. Отражение прибрежных зданий. Оптическое отражение в реке прибрежных деревьев.Отражение свечи в зеркале.

Фиалки химеры

Самыми необыкновенными, фантазийными и дорогостоящими считаются фиалки химеры – результат кропотливого труда опытных селекционеров. Специалисты получают сорт опытным путем, многократно скрещивая и высаживая до 1 тыс. экземпляров, а после отбирая цветы, которые подходят под описание химер.

Химеру легко узнать по лепесткам с красивыми узорами. Обилие расцветок просто завораживает. Такие эксклюзивные растения не размножаются вегетативным способом, так как последующие поколения полностью утрачивают признаки сорта.

К тому же химеры характеризуются повышенной подверженностью к различным заболеваниям и поражениям вредителями. Такие сорта требуют повышенного внимания и тщательного ухода. Хотя чтобы полюбоваться такой красотой стоит соблюсти все правила их выращивания. Эксклюзивные домашние фиалки химеры – настоящее сокровища для коллекционеров.

Сегодня селекционеры работают над ароматом комнатных фиалок, так как их дикие родственники, к сожалению, не источают практически никакого запаха.

Lavender Swirls

Сияющий колокольчик

Причудница

Kilauea sport

Определение понятия и виды

Симметрия в архитектуре ― одинаковое (зеркальное) расположение объектов или их частей относительно оси. Она олицетворяет равенство, неизменность. Понятие симметрия появилось очень давно. Если внимательно присмотреться, то можно увидеть, что гармония присутствует не только в архитектуре, но и в живом мире тоже.

Есть несколько видов симметрии: осевая, зеркальная, центральная. Их описание приведено в таблице.

Центральная	Наличие центра, относительно которого по обе стороны располагаются точки одного объекта. При этом все они симметричны друг другу
Зеркальная	Объекты располагаются относительно плоскости
Осевая	Объекты располагаются гармонично относительно прямой, которую разделяют на отражательную и вращательную

Диссимметрия и асимметрия

Идеальной симметрии не существует в природе. Непрекращающаяся эволюция, воздействие внешнего мира ー все это влияет на нее.

Для диссимметрии присуща частичная несоответственность некоторых элементов в композиции. Части могут находиться в произвольном порядке, не выходя за рамки симметричной композиции.

А есть ли у вас в городе симметрично построенные

Средневековые замки Европы построены в подобном стиле (замок Гродно, замок Бретонских герцогов). Храм Василия Блаженного в Москве тоже подчиняется принципу асимметрии.

Массовое градостроительство сегодня вытеснило симметрию, предоставив диссимметрии и асимметрии ведущую роль. Все чаще архитекторы в создании своих проектов используют именно эти два приема. Но в результате получаются уникальные строения, которые не перестают удивлять.

Симметрия в архитектуре: видео.

• Подготовка кабеля к монтажу доклад

    

• Возникновение и развитие французского гражданского буржуазного права доклад

    

• Доклад по химии 7 класс на тему минералы

    

• Медицинские роботы доклад 6 класс

    

• Доклад на тему кумыки

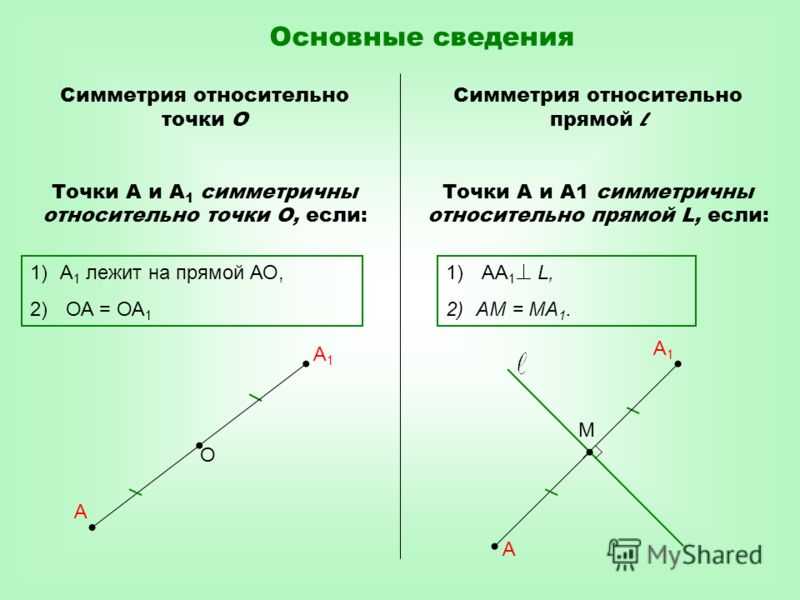
Центральная симметрия

3.1
Основные определения

Определение
.

Две точки А и А 1
называются симметричными относительно
точки О, если О — середина отрезка АА 1 .
Точка О считается симметричной са­мой
себе.

Определение.

Фигура
называется симметричной относительно
точки О, если для каждой точки фигуры
симметричная ей точка относительно
точки О также принадлежит этой фигуре.

3.2
План построения

Построение
треугольника симметричного данному
относительно цен­тра О.

Чтобы построить
точку, симметричную точке А
относи­тельно
точки О
,
достаточно провести прямую ОА
(рис. 46)
и по другую
сторону от точки О
от­ложить
отрезок, равный отрезку ОА
.
Иными
словами,

точки А
и
;
В и
;
С и

симметричны
относительно некоторой точки
О. На рис. 46
по­строен треугольник, симметричный
треуголь­нику ABC
относительно
точки О.
Эти
треугольники равны.

Построение симметричных точек
относительно центра.

На рисунке точки М
и М 1 ,
N и N 1
симметричны относительно точки О, а
точки Р и Q не симметричны относительно
этой точки.

Вообще фигуры,
симметричные относительно некоторой
точки, равны.

3.3
Примеры

Приведём примеры
фигур, обладающие центральной симметрией.
Простейшими фигурами, обладающими
центральной симметрией, является
окружность
и паралле­лограмм.

Точка О называется
центром симметрии фигуры. В подобных
случаях фигура обладает центральной
симметрией. Центром
симметрии окружности является центр
окружности, а центром симметрии
параллелограмма- точка пересечения его
диаго­налей.

Прямая также обладает
центральной симметрией, однако в отличие
от окруж­ности и параллелограмма,
которые имеют только один центр симметрии
(точка О на рисунке) у прямой их бесконечно
много — любая точка прямой является её
центром симметрии.

На рисунках показан
угол симметричный относительно вершины,
отрезок сим­метричный другому отрезку
относительно центра А

и четырехугольник симметрич­ный
относительно своей вершины М.

Примером фигуры, не имеющей центра
симметрии, является треугольник.

Почему светит Солнце

Свечение Солнца – результат выделения огромной энергии, выделяемой в результате протекания термоядерной реакции в её ядре. Вещества тратится мало, энергии выделяется много (в миллионы раз больше, чем при обычном горении).

Раньше считалось, что Солнце светит из-за горения элементов, входящих в его состав. Но по приблизительным подсчетам, даже грубым, оно не может «выгорать» миллиарды лет, Солнце должно было потухнуть совсем давно, растеряв массу, тем самым нарушив гравитационное равновесие в системе планет. Но Солнце светит уже миллиарды лет и не собирается гаснуть в ближайшее время.

История происхождения фиалки

Фиалка – однолетнее или многолетнее растение с плотной махровой листовой пластиной и мелкими соцветиями. Селекционерами получено большое количество сортов и гибридов, которые отличаются цветом бутонов и размером. Однако основным достоинством растения является их способность к цветению. Фиалка цветет долгий период – до 9 месяцев, при этом время года не влияет на этот процесс.

Легенды, связанные с фиалкой

С сенполией связано множество легенд и поверий, которые объясняют ее происхождение. Древнегреческие мифы рассказывают историю цветка фиалки. Однажды Аполлон испепелял своими жаркими лучами нежную нимфу. Девушке пришлось просить защиты у могущественного Зевса. Тот сжалился и обратил ее в красивую фиалку, укрыв от солнечных лучей в зарослях леса. Он спрятал красавицу так, что никто не мог видеть и любоваться ею.

Так продолжалось до тех пор, пока цветок не обнаружила Персефона. Она сорвала букет. На обратном пути ее украл Аид. Персефона испугалась и выронила цветы. Они просыпались с Олимпа на землю.

История появления в России

История возникновения комнатной фиалки в нашей стране началась с появления цветка в Европе. В 1893 году она была впервые представлена в Германии. В России об уникальном цветке узнали в середине XX века. Самая большая коллекция диких и селекционных экземпляров была собрана сотрудниками Ленинградского государственного университета. Позже, в 1962 году разведением и коллекционированием фиалок занялась семья Макуни. Супружеская пара занималась селекцией сенполий более 30 лет. За этот период они смогли вывести свыше сотни видов.

Родина цветка

Родиной сенполии является Африка, однако точное место назвать сложно. Впервые ее нашли в Танзании. Чаще цветок можно обнаружить в Японии, Андах, на севере Америки. Некоторые разновидности населяют субтропические регионы Бразилии, Южную Африку. Также сенполия произрастает в Новой Зенландии, в Европе, а в России встречается в южных районах Сибири. Любые виды в естественной среде обитания предпочитают открытую, слегка притененную местность умеренного климата. Для правильного роста и развития растения требуется влажный климат.

Биологическая классификация

Виды объединены в отдельный род. Их относят к травянистым растениям семейства геснериевые. Исходя из строения растения, фиалку классифицируют следующим образом:

• царство – растения;
• отдел – цветковые;
• класс – двупольные;
• порядок – ясноткоцветные;
• семейство – геснериевые;
• род – сенполии.

К иным видам классификации относят характеристику по размеру розетки, формы цветка, оттенкам бутонов, окрасу и форме листовой пластины.

Симметрия Солнца и Луны

Учитывая, что диаметр солнца составляет 1,4 миллиона километров, а диаметр луны всего 3,474 километра, очень сложно представить себе, что Луна может закрывать собой солнечный свет и давать нам около пяти солнечных затмений каждые два года.

Так как же это всё-таки происходит?

По совпадению, несмотря на то, что ширина солнца примерно в четыреста раз больше ширины луны, оно расположено от нас в четыреста раз дальше, чем луна. Симметрия этого соотношения приводит к тому, что нам кажется, что солнце и луна, одинаковые по размеру, если смотреть с Земли, поэтому луна может с лёгкостью блокировать солнце, когда они находятся на одной линии по отношению к Земле.

Расстояние от Земли до солнца, конечно, может вырасти во время её выхода на орбиту, и когда в это время случается затмение, мы можем полюбоваться ежегодным или неполным затмением, так как солнце не полностью закрыто. Но каждый год или два, всё становится абсолютно симметричным, и мы можем посмотреть на великолепное событие, которое мы называем полным солнечным затмением.

Проект по теме «Симметрия». математика 6 класс.

Проект по теме «Симметрия».

математика 6 класс.

Основные положения концепции модернизации российского образования подчёркивают необходимость создания целостной системы универсальных знаний , умений и навыков , самостоятельной деятельности и личной ответственности обучающихся. Академик РАО В.С. Лазарев считает , что для улучшения результатов образования в части развития способностей и умений обучающихся должен быть изменён способ обучения.

Обучающийся должен развивать способность самостоятельно ставить учебные цели, проектировать пути их реализации , контролировать и оценивать свои достижения. По моему мнению, проектно- исследовательская деятельность обучающихся относится к одному из эффективных способов построения образования, направленного на развитие личности. Так же , результаты проектно-исследовательской деятельности выражаются в категории компетенции и связаны с обобщёнными способами действий ( универсальных учебных действий). Основная идея образовательной технологии проектной деятельности состоит в развитии познавательной активности обучающихся к окружающему миру и к самому себе . Одними из технологий рекомендованных к использованию в школе, которые были представлена в материалах Московской Академии повышения квалификации и профессиональной переподготовки работников образования, федерального оператора Приоритетного национального проекта «Образование» являются

Технология решения исследовательских задач(ТРИЗ)

иисследовательские и проектные методы ;

Можно выделить два направления применения технологии проектно-исследовательской деятельности: в урочной и внеурочной деятельности обучающихся. Я бы хотела рассказать о примере минипроекта в урочной деятельности по математике , по теме «Симметрия» для учеников 6 класса , обучающихся по УМК Дорофеева. Все исследования на уроке носят предметных характер и направлены на изучение программного учебного материала. На этапе закрепления , систематизации и коррекции знаний я предлагаю обучающимся 6 класса проект , который начинается на уроке и заканчивается дома . Проекту предшествует определённая работа :

1. На предметной неделе для учащихся 5-6 классов проводится беседа «Что я знаю о проектах?» . Учитель рассказал об основных понятиях , связанных с проектной и исследовательской деятельностью, обучающиеся поделились своим опытом из начальной школы участия в проектах и ученики 9 класса представили свой проект по математике «Удобно ли расположена моя школа?» , с которым они победили в районном конкурсе проектов.
2. Шестиклассники познакомились с памяткой для обучающихся « Что я должен знать о проекте? ».

Данный проект я рассматриваю как подготовительный или тренировочный для учеников , чтобы в дальнейшем они могли сами выбирать самостоятельно темы , формулировать проблемы и гипотезы проекта . Но я считаю , что творчество не может развиваться на пустом месте , оно базируется на опыте.

ПРОЕКТ по МАТЕМАТИКЕ

Участники проекта:(фамилия имя , класс)	___________________________________________ 6 класс
Руководитель проекта:	Федосеева О.В.
Цели проекта:	Научиться рисовать симметричные фигуры , достраивая их и используя ось симметрии; Научиться рисовать сложные фигуры симметрично данной точки;
Задачи проекта:	Дорисовать симметричные фигуры, используя ось симметрии; Нарисовать сложную фигуру симметричную данной , относительно точки О; Скопировать по клеточкам сложные фигуры ; Сделать вывод о возможности или невозможности построения центра симметрии сложной фигуры.
Ответить на вопросы:
Что такое симметрия?
Какие виды симметрии мы изучили на уроках математики?
Какие виды симметрии я буду рассматривать при выполнении проекта?
Почему по вашему мнению, нужно выполнить данных проект ?
Выполните задания проекта
Дорисуйте симметричные фигуры относительно заданной прямой. Каждую фигуру можно выполнить одним цветом.
Скопируйте фигуру задания № 2 на тетрадный лист .Нарисуйте фигуру , симметричную данной , относительно точки О. Точку О поставить произвольно. Наклейте тетрадный лист с получившимися фигурами на лист А4.
Скопируйте фигуру задания № 3 на тетрадный лист и постройте центр симметрии данной фигуры. Можно ли его построить ? Запишите вывод и пояснение : Почему можно или нельзя. Наклейте тетрадный лист с получившейся фигурой и вашими выводами на лист А4.

ЗАДАНИЕ № 1.

ЗАДАНИЕ № 2.

ЗАДАНИЕ № 3.