Реферат на тему: осевая и центральная симметрия

Осевая и центральная симметрия

Бусинки красные свисают, из кустов на нас глядят. Очень любят бусы эти, дети, птицы и медведи. Прочитав эти строки, можно догадаться, что речь пойдет о малине. Каждый человек лечил свою простуду при помощи малинового варенья.

Джейн Остин родилась в Англии 16 декабря 1775 года. С детства родители девочки привили ей любовь к классическим произведениям.

Драцена – довольно популярное декоративное растение. Часто модно встретить его на подоконниках квартир и офисов. Имеет несколько подвидов, различающихся размером и расцветкой, благодаря чему подходит как для небольшого уголка в квартире,

Реферат на тему иоганнес брамс
Переоборудование жилых и нежилых помещений реферат
Лидерство в семье реферат
Социальная структура информационного общества реферат
Реферат сделки с жилыми помещениями

Центральная симметрия

Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.

Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.

Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии

Осевая симметрия

Определение 2

Точки $A$ и $A_1$ называются симметричными относительно прямой $a$, если эта прямая перпендикулярна к отрезку ${AA}_1$ и проходит через его центр (рис. 1).

Рисунок 1.

Рассмотрим осевую симметрию на примере задачи.

Пример 1

Построить симметричный треугольник для данного треугольника относительно какой-либо его стороны.

Решение.

Пусть нам дан треугольник $ABC$. Будем строить его симметрию относительно стороны $BC$. Сторона $BC$ при осевой симметрии перейдет в саму себя (следует из определения). Точка $A$ перейдет в точку $A_1$ следующим образом: ${AA}_1\bot BC$, ${AH=HA}_1$. Треугольник $ABC$ перейдет в треугольник $A_1BC$ (Рис. 2).

Рисунок 2.

Определение 3

Фигура называется симметричной относительно прямой $a$, если каждая симметричная точка этой фигуры содержится на этой же фигуре (рис. 3).

Рисунок 3.

На рисунке $3$ изображен прямоугольник. Он обладает осевой симметрией относительно каждого своего диаметра, а также относительно двух прямых, которые проходят через центры противоположных сторон данного прямоугольника.

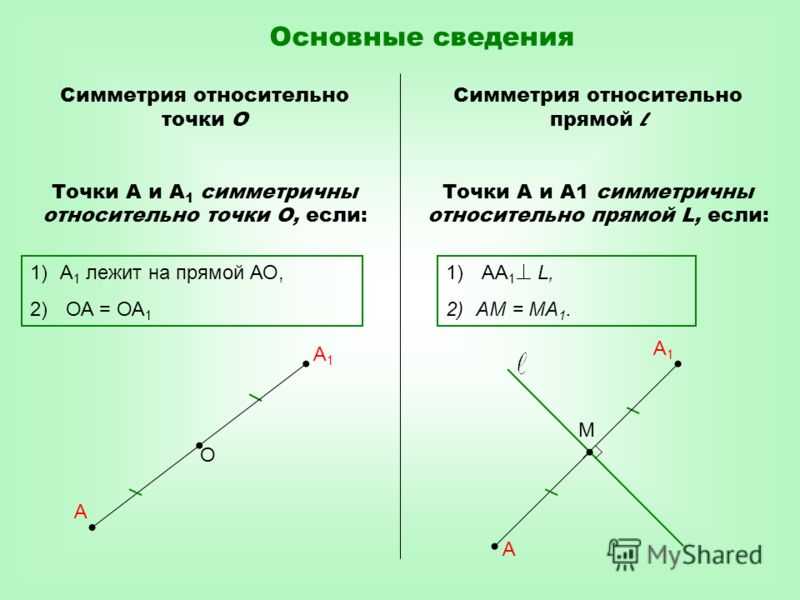
Симметрия, симметрия относительно прямой

Правило 1

Точки A и A1 называется симметричными относительно точки О,

если O AA1 и AO = OA1. Точка, симметричная точке O, есть сама точка O.

Симметрия относительно точки O (= центральная симметрия) — преобразование фигуры F в фигуру F1, при котором каждая ее точка X переходит в точку X1, симметричную относительно данной точки O — центра симметрии.

! Симметрия относительно точки является движением.

Если симметрия относительно точки O переводит фигуру F в себя, то эта фигура называется центрально — симметричной. Параллелограмм — центрально — симметричная фигура. Его центр симметрии — точка пересечения диагоналей.

Правило 2 Точки A и A1 называются симметричными относительно прямой l, если отрезок AA1 ? l и AA1 делится прямой l пополам. Если точка X l, то симметричная ей точка есть сама точка X.

Симметрия относительно прямой l (= осевая симметрия) — преобразование фигуры F в фигуру F1, при котором каждая ее точка X переходит в точку X1, симметричную относительно данной прямой l — оси симметрии.

!Симметрия относительно прямой является движением.

Если симметрия относительно прямой l переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой l.

Ось симметрии ромба — прямые, на которых лежат его диагонали.

1.3. Поворотная симметрия

Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.

Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой.

Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».

На рисунке 2.7. даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.

Что означает симметрия в разных науках?

Биология

В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии

Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.

Химия.

Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.

Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.

Для просмотра онлайн кликните на видео &cudarrr;

8 класс, 9 урок, Осевая и центральная симметрия Подробнее

Геометрия 8 Осевая и центральная симметрия Подробнее

Геометрия 8 класс: Осевая и центральная симметрии Подробнее

48. Осевая и центральная симметрии Подробнее

Математика 6 Осевая симметрия Подробнее

9 класс, 30 урок, Понятие движения Подробнее

Осевая симметрия, как начертить треугольники симметрично Подробнее

Геометрия 9 класс (Урок№28 — Отображение плоскости на себя. Понятие движения. Наложения и движения.) Подробнее

6 класс, 26 урок, Симметрия Подробнее

Геометрия 8 класс 7-8 неделя Трапеция. Осевая и центральная симметрия. Подробнее

Математика| Подобие треугольников Подробнее

Хитрости в решении геометрических задач в ОГЭ Подробнее

Почему животные симметричны? Подробнее

Математика | КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? Подробнее

МАТЕМАТИКА | ТОП-5 ОШИБОК Подробнее

Математика| Геометрия 7 класса в одной задаче Подробнее

ГЕОМЕТРИЯ | Хочешь находить площадь любой фигуры? Подробнее

9 класс, 32 урок, Параллельный перенос Подробнее

голоса

Рейтинг статьи

Применение законов симметрии человеком

Увидев проявление симметрии в природе, мне захотелось узнать, применяет ли человек эти узоры в своих творениях.

Симметрию можно найти почти везде, если знать, как ее искать. С древних времен многие народы владели концепцией симметрии в широком смысле слова — как о балансе и гармонии. Творчество людей во всех своих проявлениях стремится к симметрии. С помощью симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство». Г. Вейль понимал симметрию как «неизменность объекта при определенном виде преобразования; объект является симметричным в том случае, если его можно подвергнуть некоторой операции, после которой он будет выглядеть так же, как и до преобразования. Г. Вейль посвящен определенная глава с декоративной симметрией. Мы находим упорядоченность и подчиненность определенного набор правил в узорах и орнаментах.

В огранке драгоценных камней нельзя не увидеть симметрию. Многие огранщики пытаются придать алмазу форму тетраэдра, куба, октаэдра или икосаэдра. Поскольку гранат содержит те же элементы, что и куб, он высоко ценится ценителями драгоценных камней. Художественные изделия из граната были найдены в могилах Древнего Египта, относящихся к додинастическому периоду (более двух тысячелетий до нашей эры).

В собраниях Эрмитажа особое внимание уделяется золотым украшениям древних скифов. Произведения из золотых венков, диадем, дерева и украшенных драгоценными красно-фиолетовыми гранатами необычайно тонки.

Одно из наиболее очевидных применений законов симметрии в жизни — это строительство архитектуры. Это то, что мы видим чаще всего. В архитектуре оси симметрии используются как средство выражения архитектурного замысла. Примеров использования симметрии в архитектуре немало, один из которых — замечательный Новосибирский театр оперы и балета. И даже здесь, в городе Купино, есть симметричное здание — здание Администрации Купинского района.

Другой пример использования человеком симметрии в своей практике — техника. В технике наиболее четко указываются оси симметрии там, где требуется оценить отклонение от нулевого положения, например, у штурвала грузовика или штурвала корабля. Или одним из важнейших изобретений человечества, имеющим центр симметрии, является колесо, а пропеллер и другие технические средства также имеют центр симметрии.

Даже там просматривается симметрия, на которую я никогда не обращал внимания. Например, если вы поместите буквы перед зеркалом, расположив его параллельно линии, вы заметите, что буквы с горизонтальной осью симметрии можно прочитать в зеркале. А вот те, у которых ось расположена вертикально или вообще отсутствует, становятся «нечитаемыми».

Есть языки, в которых стиль знаков основан на наличии симметрии. Итак, в китайской письменности иероглиф означает именно истинную середину.

Что такое симметрия

Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.

В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.

Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.

Рис. 1 Фигуры, обладающие симметричностью

Осевая симметрия

Сегодня на уроке мы вспомним такое понятие как осевая симметрия на плоскости, введём понятие осевой симметрии в пространстве, проверим, будет ли осевая симметрия движением пространства.

Давайте вспомним, что фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Прямая называется осью симметрии фигуры. Про такую фигуру говорят, что она обладает осевой симметрией.

Давайте приведём примеры таких фигур из жизни и геометрии.

Ещё мы давали такое определение:
Точки и называются симметричными относительно прямой , если прямая проходит через середину отрезка и перпендикулярна к этому отрезку.
Прямая называется осью симметрии.
Каждая точка прямой считается симметричной самой себе.
В курсе планиметрии мы доказывали, что осевая симметрия является движением.
Напомним это доказательство.

Пусть точки М и N – какие-нибудь точки плоскости, а точки М1, и N1 – симметричные им точки относительно прямой А. Здесь может быть несколько вариантов расположения точек на плоскости.

Рассмотрим один из таких вариантов.
По построению симметричных точек относительно прямой А, прямая А перпендикулярна прямым ММ1 и NN1 и делит эти отрезки пополам, значит, в треугольниках МОМ1 и NОN1 отрезки ОК и ОЕ будут являться медианами и высотами, проведёнными к основанию, то есть это равнобедренные треугольники.
.
.
Заменив отрезок равным ему отрезком , а отрезок – равным ему отрезком , получим, что .
Вывод: таким образом, мы доказали, что расстояние между точками М и N равно расстоянию между симметричными им точками М один и N1.
Получаем, что осевая симметрия – пример движения плоскости.
В пространстве осевой симметрией с осью мы назовем такое отображение пространства на себя, при котором любая точка переходит в симметричную ей точку относительно оси .
Теперь давайте проверим, будет ли осевая симметрия в пространстве движением пространства.

Для этого введём прямоугольную систему координат Оxyz так, чтобы ось Оz совпала с осью симметрии. Теперь давайте попробуем найти связь между координатами точки М с координатами x, y, z и точки М1 с координатами x1, y1,z1, симметричных относительно оси Оz.

Если точка М не лежит на оси Оz, то по определению оси симметрии, ось Оz проходит через середину отрезка ММ1 и перпендикулярна к этому отрезку. Поскольку Оz – середина отрезка ММ1, и абсциссы и ординаты точек оси Оz равны нулю, то можно записать, что и .

То есть , .
Условие того, что ось Оz перпендикулярно прямой ММ1 даёт нам, то что аппликаты точек М и М1 равны .
Если же точка М лежит на оси Оz, то она отображается сама на себя, по определению оси симметрии, значит, и в этом случае будут выполнятся полученные равенства.
Вывод: для симметричный точек относительно оси Оz абсциссы и ординаты противоположны, а аппликаты равны.

Возникает вопрос, а если ось симметрии совпадает не с осью Оz, а, например, Оx или Оy. Тогда связь между координатами симметричных точек М и М1 будет такая: если ось симметрии проходит через ось Оx, то точки М и М1 имеют такие координаты , .

Если осью симметрии будет ось Оy, то точки М и М1 имеют такие координаты , .

Теперь давайте рассмотрим любые две точки и . По только что доказанным формулам для координат симметричных точек получим, что точка . Точка .

Теперь давайте найдём расстояние .
Получим, что .
Теперь давайте найдём расстояние между точками и .

Очевидно, что оба эти выражения равны, то есть получим, что . То есть расстояние между точками при осевой симметрии в пространстве сохраняется, значит, осевая симметрия в пространстве также является движением, но уже не плоскости, а пространства.

Задача: найти координаты точек, в которые переходят точки , , при осевой симметрии относительно координатных осей.
Решение: сначала найдём координаты точек в которые переходит точки , , при осевой симметрии относительно оси Ох.
Если точка симметрична точке относительно оси то справедливы формулы: .
Точка отобразится в точку .
Точка отобразится в точку .
Точка отобразится в точку .
Если точка симметрична точке относительно оси то справедливы формулы: .
Точка отобразится в точку .
Точка отобразится в точку .
Точка отобразится в точку .
Если точка симметрична точке относительно оси то справедливы формулы: .
Точка отобразится в точку .
Точка отобразится в точку .
Точка отобразится в точку .
Итоги:

Сегодня на уроке мы ввели понятия осевой симметрии в пространстве. Показали, что и в пространстве осевая симметрия будет примером движения. Решили несколько задач.

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

На картинках центральная симметрия: точка O здесь — центр симметрии

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Измеряем расстояние от точки B до точки О и от точки А до точки О.
Проводим прямую из точки А через точку О и выводим ее на другую сторону.
Проводим прямую из точки B через точку О и выводим ее на другую сторону.
Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Подписи к слайдам:

Осевая и центральная симметрия Что такое осевая и центральная симметрия?

«Симметрия является той идеей,посредством которой человек на протяжении веков пытался постичь и создать порядок,красоту и совершенство» Г.Вейль

Симметричность точек относительно прямой Определение Две точки А и А 1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. A 1 A a O B A A 1 a Т AO = OA 1

Симметричность фигуры относительно прямой Определение Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. А D B C M K N P a b c

Симметричность точек относительно точки Определение Точки A и A 1 называются симметричными относительно точки О , если О – середина отрезка AA 1 . A O A B B 1 O A 1 A 1

Симметричность фигуры относительно точки Определение Фигура называется симметричной относительно точки , если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. A B C D O

Симметричность на координатной плоскости y x A B (4;3) C y x A A 1 B 1 B C C 1 (-4;3) (4;-3)

Симметричность на координатной плоскости y y x x A B C D A 1 B 1 C 1 D 1 M K K 1 M 1

Симметрия вокруг нас С симметрией мы часто встречаемся в природе

Симметрия вокруг нас Многие предметы окружающего нас мира имеют ось симметрии или центр симметрии

Математики о симметрии Математик любит прежде всего симметрию Максвелл Д. Красота тесно связана с симметрией Вейль Г. Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство Вейль Г . Для человеческого разума симметрия обладает, по — видимому, совершенно особой притягательной силой Фейнман Р.

Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство». Вывод.

Элементы небесной сферы

Небесная сфера включает в себя не только расположение всех светил, но и многие ориентиры, с помощью которых ученые могут четко определять, измерять и прогнозировать движение звезд

Важно понимать, что в большинстве расчетов сфера представляет собой лишь чертеж, на котором обозначены многие условные обозначения, рассмотренные ниже

Отвесная линия и связанные с ней понятия

Отвесная линия, также известная, как вертикальная линия, – это ось, совпадающая с положением нити воображаемого маятника (отвеса), находящегося в центре сферы. Эта линия пересекает ее в двух точках: ровно над головой наблюдателя (в зените) и под ногами (в надире). Является основной осью небесной сферы в горизонтальной системе координат.

Основная ось небесной сферы

Астрономический (истинный) горизонт – большой круг небесной сферы, плоскость которого строго перпендикулярна отвесной линии. Он делит сферу на две равные части: видимую полусферу, находящуюся выше наблюдателя и невидимую, находящуюся ниже. Ошибочно предполагать, что при наблюдении с земли истинный горизонт будет совпадать с видимым. Их положение будет отличаться из-за искривления света и того, что точка наблюдения оторвана от поверхности земли.

Астрономический горизонт

Для того чтобы ориентироваться по небесной сфере, на ней существует собственная координатная сетка, но вместо осей ординат и абсцисс на ней есть круги высот и альмукантараты.

Круг высот – это плоскость, проходящая перпендикулярно астрономическому горизонту через зенит небесной сферы, надир и небесное светило. Альмукантарат же в свою очередь представляет собой плоскость параллельную истинному горизонту. Точка пересечения этих плоскостей с небесной сферой и определяет сферическую координату светила.

Суточное вращение небесной сферы и связанные с ним понятия

Ось мира схожа с осью вращения Земли. Она проходит через северный и южный полюса мира, которые могут не совпадать с точками зенита и надира. Вокруг этой прямой и вращается небесная сфера, причем строго против часовой стрелки.

Небесный экватор, как и Земной, представляет собой линию, делящую сферу на две равные части – северное и южное полушарие. Небесный экватор перпендикулярен оси мира и проходит строго через центр сферы.

Круг светила – круг, обозначающий движение Солнца по небесной сфере, который проходит через оба полушария и точку, на которой находится небесное тело.

Суточная параллель – круг небесной сферы, по которому светило совершает свое суточное движение, причем в северном полушарии все наблюдаемые светила всегда движутся против часовой стрелки, а в южном – по часовой стрелке.

Вместе круги светил и суточные параллели образуют еще одну систему координат, называемую экваториальной.

Термины, связанные с понятием “Отвесная линия” и “Вращение небесной сферы”

Так как небесный экватор и истинный горизонт – это два круга, у них есть всего 2 точки пересечения. Они называются точками запада и востока. Небесные светила всегда восходят из-за горизонта возле точки востока, а заходят возле точки запада.

Полукруг, который через точку востока соединяет северный и южный полюс называется первым вертикалом.

Параллельно отвесной линии и оси мира проходит еще одна плоскость – небесный меридиан. Он разделяет сферу на два полушария – восточное и западное.

Небесный меридиан

Полуденная линия небесной сферы – это прямая, на которой пересекаются истинный горизонт и небесный меридиан. Пересечение этой линии с небесной сферой образует еще две новые точки: точка севера, расположенная ближе к северному полюсу, и точка юга, приближенная к южному полюсу.

Годовое движение Солнца по небесной сфере

Солнце движется на небесной сфере по определенной траектории, называемой эклиптикой. Она образует круг, который отклонен от небесного экватора на 23 градуса.

Прямое восхождение и точки равноденствия

Если провести от центра линии равноденствия прямую, перпендикулярную плоскости небесного экватора, то она отметит на небесной сфере еще две важные точки – летнего и зимнего солнцестояния.

Чаще всего на схемах и моделях точки равноденствия и солнцестояния обозначаются зодиакальными символами, которые соответствовали созвездиям, в которых размещены отметки на сфере:

Весеннее равноденствие – Овен;
Осеннее равноденствие – Весы;
Зимнее солнцестояние – Козерог;
Летнее солнцестояние – Рак

Еще одна важная прямая на небесной сфере – это ось эклиптики. Она перпендикулярна плоскости эклиптики и проходит через центр сферы, отмечая на ней две точки – северный и южный полюса эклиптики.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

На рисунках осевая симметрия: точки A и B симметричны относительно прямой a; точки R и F симметричны относительно прямой AB

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
С другой стороны прямой отложим такие же расстояния.
Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
Измеряем расстояние от вершин до точек на прямой.
Откладываем такие же расстояния на другой стороне оси симметрии.
Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Проводим через точку А прямую, перпендикулярную прямой l.
Проводим через точку В прямую, перпендикулярную прямой l.
Измеряем расстояния от точек А и В до прямой l.
Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий —
на курсах по математике в онлайн-школе Skysmart!

Какие фигуры являются симметричными?

Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.

Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.

Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.

Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.

К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.

Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.

У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.

Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.

Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.